This site uses cookies to provide you with a great user experience. By using BondbloX, you accept our use of cookies.
Bond Market News
Bond Duration – Understanding Interest Rate Risk
December 20, 2024

Bond duration is used as a key measure of interest rate risk. With the US Fed, Bank of England and other global central banks raising interest rates, understanding the concept of duration is critical for bond investors and advisors. Duration is a key metric used by professional investors to help manage risk and it forms the building block for any bond investor. In this piece, we cover all essential concepts regarding duration with examples. Investors can view bond duration on the BondEvalue App and use it as a tool to compare bonds that suit their investment objectives.
What is Duration and How do you Define It?
We know that bond prices are inversely related to interest rates. If interest rates rise, bond prices fall and if interest rates fall, bond prices rise. That said, bond duration is a metric that quantifies:
- How much a bond’s price is expected to change by, if interest rates change by 100bp – known as Modified Duration (more on this below)
- The time it takes for the bond to repay all of its coupons and principal factoring in the time value of money – known as Macaulay’s Duration (more on this below)
A Detailed Understanding of Duration
Duration (as in Macaulay’s Duration) gives us an estimate of how much time it takes to recoup the cost/price of the bond before maturity. Since each cash flow from the bond is given a time-weighted importance, the first cashflow helps recoup a portion of the cost of the bond in lesser time than subsequent cashflows. The same applies to the second and later cashflows, that help recoup a portion of the bond’s cost in lesser time than the cashflows that follow them.
The concept of bond duration can be understood via the example of a fulcrum as shown below:
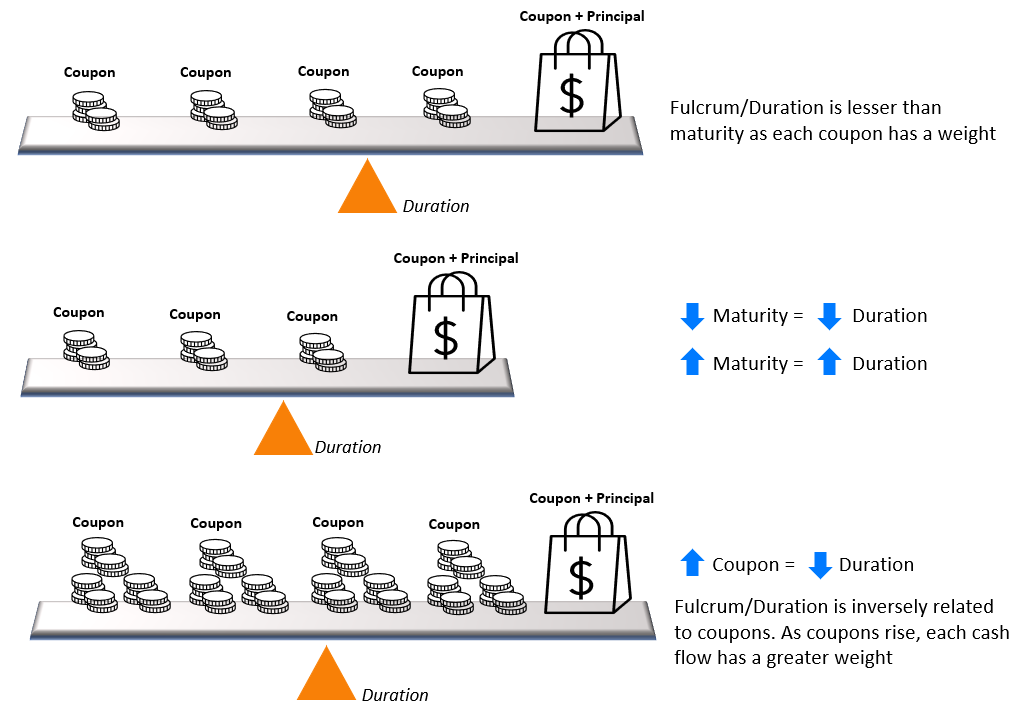
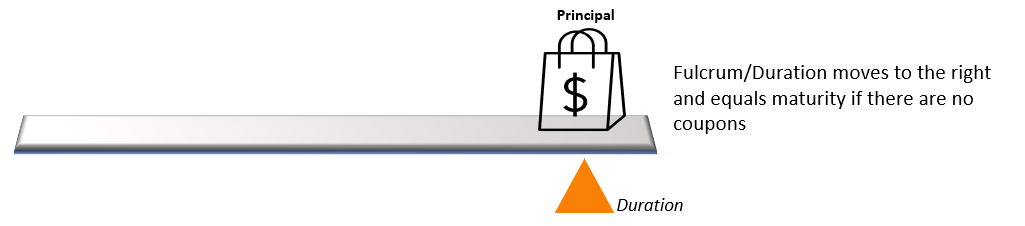
Rules of Duration
Now that we have an intuitive understanding of duration, below are the inferences that can be made:
- For an interest paying bond, the duration will always be lesser than the maturity
- For a zero-coupon bond/non interest paying bond, the duration will equal the bond’s maturity
- Duration decreases as coupons increase; duration increases as coupons decrease
- Duration decreases as yields increase; duration increases as yields decrease
- Perpetual bonds have a finite duration
Types of Duration
Duration is a mathematically calculated measure. Whilst we now have an understanding of the concept, let us look at the different types of duration measures.
Macaulay’s Duration
Macaulay’s Duration measures the time it takes to recoup the cost of the bond giving a weight to each cash flow. Akin to a bond’s maturity, this is also measured in years. Thus, a bond trading at par with a 5 year maturity and Macaulay’s Duration of 4.55 years tells us that the investor who invests $100 in a bond will recoup his/her investment in 4.55 years. See the appendix below for an example with the calculations on MS Excel.
In the colloquial sense, the word duration is thought of in terms of time and people are susceptible to mistake this measure as the bond’s maturity. A bond’s maturity is simply the time taken until a bond’s interest payments cease and its principal is paid back. However, a bond’s maturity does not factor in the time value of money where $1 today is worth more than $1 tomorrow and thereafter!
Modified Duration
Modified Duration tells us how much a bond’s price will change with respect to a change in yield. Thus, a bond trading at par with a modified duration of 4.33 years tells us that the bond’s price will rise by 4.33% if interest rates fall by 100bp (1%). It also indicates that the bond’s price will fall by 4.33% if interest rates rise by 100bp. The calculation of Modified Duration is an offshoot of Macaulay’s Duration. Here, we divide Macaulay’s Duration by (1 + yield to maturity) due to differentiation formulas in calculus. The appendix below shows the calculation of Modified Duration on MS Excel.
Effective Duration
A limitation of both Macaulay’s Duration and Modified Duration is that they do not incorporate the impact of options. For example, bond with a call option can be called back before its maturity date. Effective Duration accounts for the optionality in a bond. Effective Duration thus takes the price of the bond if yields increase or decrease by a certain quantum. See the appendix below for the formula to calculate effective duration.
How Can Investors Use and Interpret Duration?
Now that we have a good understanding of duration (modified duration), we can agree that it is a measure of price risk. As we established earlier, it is the price sensitivity of the bond with respect to a change in the underlying interest rate. One of the simplest way to use duration while investing in a bond is to multiply the duration with the change in yield. Let’s look at examples below from the BondEvalue App.
We first consider Vedanta’s 9.25% dollar bond maturing in April 2026. The bond’s price is about $84 for a par value of $100, a yield to maturity (YTM) of 14.92% and a duration of 3.09 as of May 9, 2022. Let’s assume that an investor buys the bond at $84 and expects the yield to rise by 100bp to 15.92%. In this case, the bond’s price would fall by 3.09% to $81.4. Similarly, if the yield is expected to fall by 100bp to 13.92%, then the price would rise by 3.09% to $86.6. This is the simplest interpretation.
However, another crucial way an investor can use duration is to calculate how much would the yield/interest rates need to rise to lose all of the bond’s yield/return. Dividing the yield by the duration, you would get the change in yields that would wipe out your bond’s 14.92% yield/returns. Thus, a 483bp or 4.83% (14.92% ÷ 3.09) change in the yield/interest rates would essentially wipe out the investor’s return from the bond.

Let’s take another example of Amazon’s 1% bond due May 2026 shown below. The bond has a similar maturity to Vedanta’s bond above. In this case, dividing the yield by the duration, a 1bp or 0.01% (3.48% ÷ 3.84) change in the yield/interest rates would essentially wipe out the investor’s 3.48% yield/return from the bond.

As you can observe, while Amazon (A1/AA-/AA) might be a safer bet than Vedanta (B2/B-) in terms of credit ratings, a smaller/minor change in yields could hurt their investment in Amazon a lot more than in Vedanta. This reiterates our earlier conclusion, where a higher yield benefits an investor as the duration is low, implying less price risk for Vedanta’s bond. It also emphasizes that Investment Grade (IG) bonds have a higher duration risk than High Yield (HY) bonds.
Limitation of Duration as a Metric
Duration, despite its simple conceptual understanding is not a perfect metric. If you look with a keen eye on duration, you will notice that there is a flaw. Duration assumes that a bond’s price rises/falls by the same amount for a given change in yields. In other words, it is a linear metric. A bond duration of 5 years would imply that the bond’s price changes by 5% if yields go up or down by 100bp. In practice, bond prices do not move linearly but are convex by nature. Bond prices gain more than they fall for the same change in yields i.e., the price gain for a 100bp fall in yields is more than the price loss for a 100p rise in yields. This incremental benefit on the upside for bond prices is known as ‘bond convexity’.
Appendix
-
Macaulay’s Duration and Modified Duration Calculations
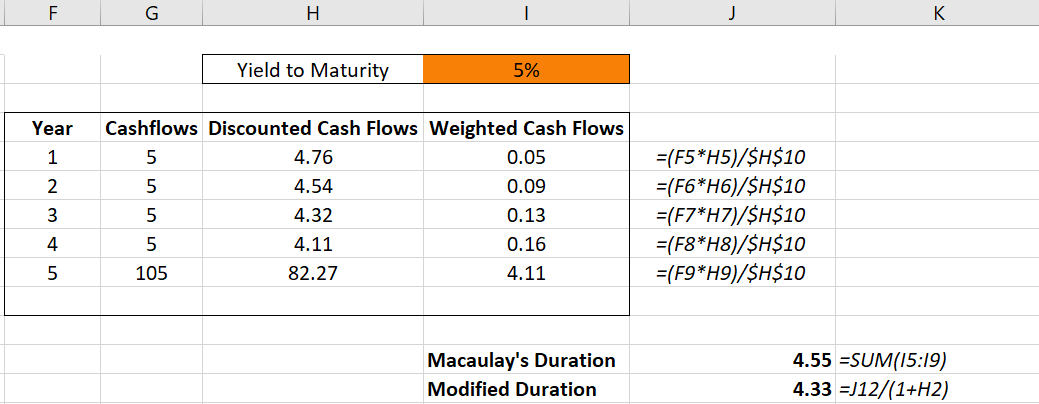
-
Effective Duration Calculation
Go back to Latest bond Market News
Related Posts:
What to Look for When Buying Bonds
December 4, 2024

Masala Bonds – Everything You Need to Know
December 17, 2024
New Bond Issue Process – Explained
December 13, 2024







